久方ぶりの地理講義の更新である。
今回、紹介するのは、地理の中で最も重要であると思われることである。
すなわち、地球は丸いということだ。
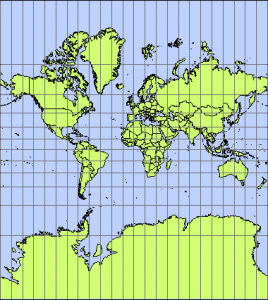
これが、皆さんがよく見慣れている地図であると思う。
実際には、極地域は描いていないので、ちょっと縦長な気がするかと思うが。
ただ、最初に描いたとおりに地球は、丸い。
この地図から、地球は丸いということを実感できるだろうか。
やはり、地球は丸いということを実感するためには、
これらが必要になってくる。
面白い地球儀が検索したら、いっぱい出てきたので、いっぱい載せてしまったが(Amazonのリンクになっているので、実際に買えます)笑
つまり、丸い地球を表すためには、平面の地図(2D)ではなく、こういった地球儀(3D)が必要になってくるはずである。
それでは、最初に載せたような平面の地図(2D)は、丸い地球を表してはいないのであろうか。
答えは…
否である。
地図は、地球を表している。
地図は、2Dであるのに、3Dの地球を表しているから、すごいのである。
もちろん、2Dで、3Dの地球の全てを表すことはできない。
しかし、一定のルールに従って、目的に応じた正しさを地図は表現しているのだ。
その一定のルールこそ、投影法と呼ばれるものである。
投影法とは、その文字の通り、照明を当てて、地球を幕に投影したものを地図とするという考え方である。
当然、地球に照明を当てることはできないし、仮に太陽を照明と考えたとしても、それを映す超巨大な幕などはない。だが、そう仮定して考えることによって、地球をより正しく表す方法を思いつくことができたのである。
ちなみに、一番最初に挙げた地図は、16世紀にオランダの地理学者であるグラルドゥス=メルカトルによって考案されたメルカトル図法である。
代表的な投影法の考え方は、以下のような形である。
- 方位図法
地球に対して、ある点から光を当てて、それに対して、垂直な平面の幕に影を投影する方法。
影は丸い形となり、中心の点からの任意の点への方角が正しくなる他、中心の点から任意の点への距離が正しくなる場合もある。
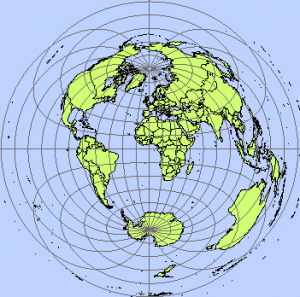
代表的な投影法は、正距方位図法であり、国連のマークなどが最も有名である。
その他、ランベルト正積方位図法や心射方位図法などが挙げられる。
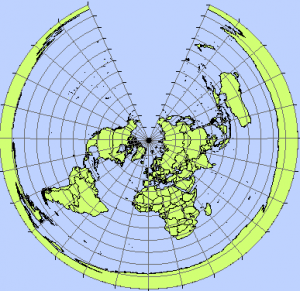
これが正距方位図法である。
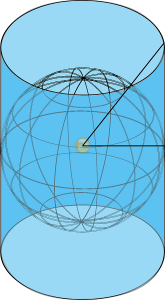
- 円筒図法
地球に幕を巻き、円筒状にしたものに影を投影する方法。
影は、四角形となる。
幕に接している部分の左右の長さが正しい長さになり(全てが地球に接しているため)、そこから上下に離れて行くにつれて、影が伸びるため、長さも伸びていく。
代表的な投影法は、メルカトル図法であり、おそらく日本人が最も見慣れた世界地図だと思われる。
その他、UTM図法(ユニバーサル横メルカトル図法)やランベルト正積円筒図法などが挙げられる。
最初に載せたとおり、これがメルカトル図法である。
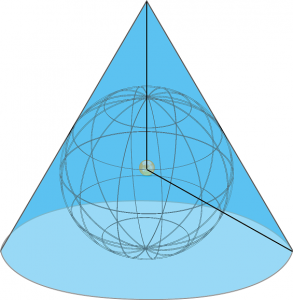
- 円錐図法
地球に対して、斜めになるように幕を巻き付け、円錐形にしたものに投影する方法。
影は、扇状になる。
円錐の頂点の部分を中心とした扇形の地図は、中心からの任意の点の距離が正しくなる。
代表的な投影法は、正距円錐図法であるが、あまりお目にかかる機会は多くない。
その他、ランベルト正角円錐図法などが挙げられる。
これが正距円錐図法である。
このように、地球を地図に起こす投影法は、数多く考案されている。
それはなぜか。
正積や、正距方位、正角など、正しい○という言葉が踊るとおり、地図は、2Dである以上、3Dの地球の全てを正しく表すことはできない。
よって、何の正しさを取るのか、ということで、他の正しさを捨てて、利用用途に応じて、正しいものを選択するのだ。
例えば、正距方位図法は、中心から任意の点への距離と方位が正しい図法だ。
しかし、正積図法ではないため、面積は正しくない。
正角図法ではないため、任意の2点の角度は正しくない。
一方、メルカトル図法は、正角図法だ。
つまり、距離も方位も面積も正しくはないが、地図上の好きな2点を選んだときに、その角度は正しくなる。
これは、メルカトル図法が作られたのは、大航海時代であり、まだ地球の姿、世界の全貌が明らかになる前の時期に、考案された投影法だ。
正角とは、航海に用いていた天測機器の角度と一致するということであり、その角度に従って船を進めれば、その場所にたどり着けるという、海図のための図法であった。
それに対して、現在日本などで使われている地図には、UTM図法(ユニバーサル横メルカトル図法)が用いられている。
くわしくは、別途機会を設けて語るつもりだが、経度に沿うようにして、円筒を作るメルカトル図法に対して、緯度に沿うようにして円筒を作ることによって、緯度方向に距離が正しい地図を作ろうという試みだ。
緯度方向に距離が正しい地図であり、かつごく狭い範囲であるならば、経度方向の伸びも無視できるため、正距や正積であるといった考え方の投影法であり、日本の地形図にも用いられている。
このように、目的に応じて、さまざまな投影法を使い分けて、さまざまな地図を作成しているのである。






1件のピンバック